badper.blogg.se - Khan academy graphing inequalities

Given a solution of the heat equation, the value of u(x, t + τ) for a small positive value of τ may be approximated as 1 2 n times the average value of the function u(⋅, t) over a sphere of very small radius centered at x.

The function f (t,x) can for example describe the concentration of a chemical as a function of time t and position x.

Nicolson, A practical method for numerical …. NOTE: Given y = f(x), its derivative, or rate of change of y with respect to x is defined as. This is the definition, for any function y = f(x), of the derivative, dy/dx. Differentiation From First Principles - Revision Maths - Maths …. Furthermore, you can compute the derivative using the product . If f is nonzero and differentiable (at a point x=a), then so is the reciprocal 1/f (at x=a). I can solve the math problem for … Derivative of Reciprocal (1/f) - Expii. The rule for differentiating an exponential function is that for f(x)=eu Solve math. How to differentiate e^2x+1 - Math Questions. First create a function that represents the nonlinear constraint. Find the minimum of Rosenbrock's function on the unit disk, $||x||^2 \le 1$. MATLAB fmincon - Nonlinear Optimization - MathWorks. Derivative by First Principle This is called differentiation from first principles, (or the delta method). Find the derivative of the following functions from first principle (x-1)(x-2) (x- 1)(x- 2). Find the derivative of function from first principle | Math Lessons.

Complete step-by-step answer: Given the function $ f(x) = 3x + 2 $, we have to calculate the derivative of the function using the first . Find derivative of $ f(x) = 3x + 2 $ using the first principle of.

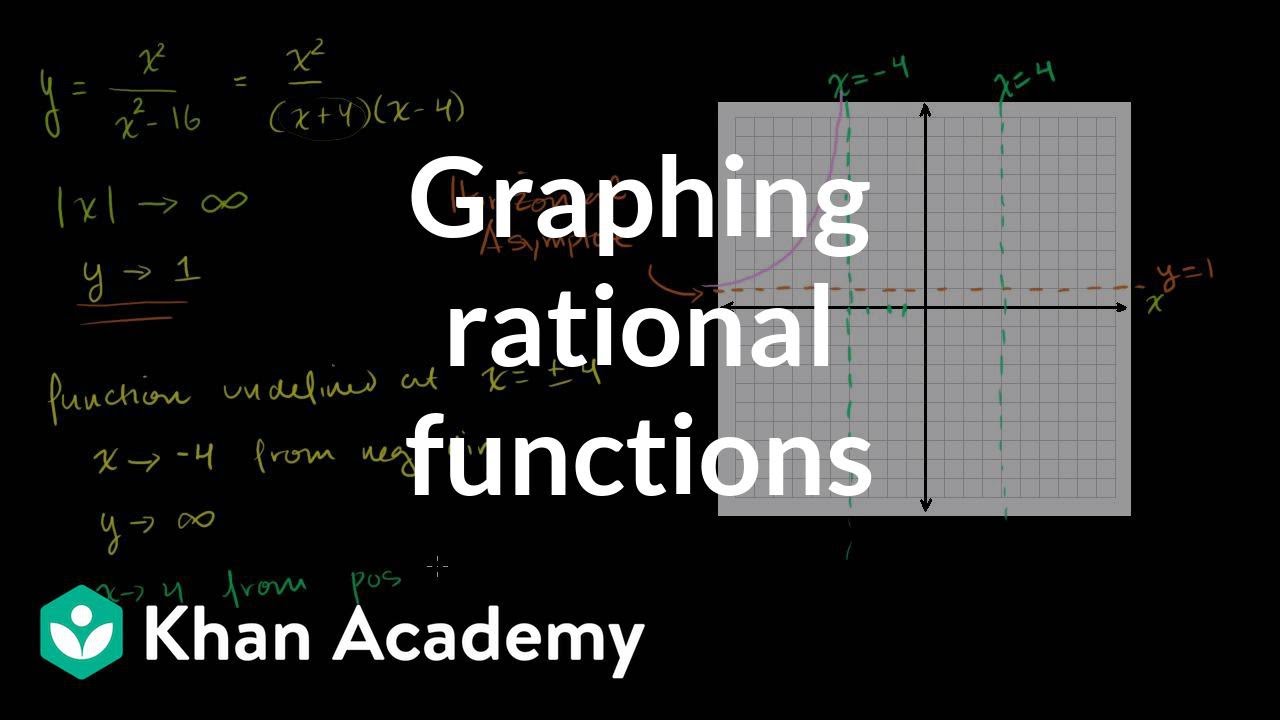
(1) where y is a function of x, y^'=dy/dx is the ﬁrst derivative with . Solve a linear equation: 4x+3=19 Solve a polynomial equation: solve x^2 + 4x + 6. Find the derivatives of the following functions using first principle.

Since this is a "y greater than" inequality, we want to shade above the line.How to Find Derivatives Using First Principle - onlinemath4all. So the border of our solution region actually looks like this:īy using a dashed line, we know where the border is but we also know that the border isn't included in the solution. The notation for a strict inequality is a dashed line. We have inequality where "y is greater than". Solve the Quadratic Equation by the Quadratic Formula.Solve the Quadratic Equation by Factoring.Solve the Quadratic Equation by Extracting Roots.Multiplying and Dividing Positive and Negative Whole Numbers.